Рис.1.
2.1. Классификация криптоалгоритмов
В зависимости от наличия либо отсутствия ключа кодирующие алгоритмы делятся на
тайнопись и криптографию.
В зависимости от соответствия ключей шифрования
и дешифрования – на симметричные и
асимметричные. В зависимости от
типа используемых преобразований
– на подстановочные и
перестановочные. В зависимости от
размера шифруемого блока – на потоковые
и блочные шифры.
2.2. Симметричные криптоалгоритмы
Симметричные криптоалгоритмы выполняют преобразование небольшого
(1 бит либо 32-128 бит) блока данных в зависимости от ключа таким образом,
что прочесть исходное сообщение можно только зная этот секретный ключ.
2.3. Симметричные криптосистемы
Симметричные криптосистемы являются полноценными программами, которые могут
на основе симметричных криптоалгоритмов кодировать и декодировать файлы
произвольной длины. Криптосистемы устраняют целый класс "потенциальных
уязвимостей" систем, использующих симметричные криптоалгоритмы.
2.4. Асимметричные криптоалгоритмы
В асимметричных криптоалгоритмах для зашифровывания сообщения используется
один ключ, а для расшифровки другой. Ключ шифрования известен всем, но
выполняемое преобразование необратимо, поэтому зашифрованный текст не может
прочесть никто, кроме получателя – именно он один знает
второй (закрытый) ключ.
2.5. Асимметричные криптосистемы
Поскольку асимметричные криптоалгоритмы очень медленны, в реальных системах
используются быстрые надежные симметричные криптоалгоритмы по схеме с
ключом сеанса. А вот сам ключ сеанса кодируется асимметричным криптоалгоритмом
с помощью открытого ключа получателя. Подобная система обладает всеми свойствами
асимметричного криптоалгоритма и очень высоким быстродействием.
Сама криптография не является высшей ступенью классификации смежных с ней дисциплин. Наоборот, криптография совместно с криптоанализом (целью которого является противостояние методам криптографии) составляют комплексную науку – криптологию.
Необходимо отметить, что в русскоязычных текстах по данному предмету встречаются различные употребления основных терминов, таких как "криптография", "тайнопись" и некоторых других. Более того, и по классификации криптоалгоритмов можно встретить различные мнения. В связи с этим автор не претендует на то, что его вариант использования подобных терминов является единственно верным.
В отношении криптоалгоритмов существует несколько схем классификации, каждая из которых основана на группе характерных признаков. Таким образом, один и тот же алгоритм "проходит" сразу по нескольким схемам, оказываясь в каждой из них в какой-либо из подгрупп.
Основной схемой классификации всех криптоалгоритмов является следующая:
Весь дальнейший материал будет посвящен криптографии с ключом, так как большинство специалистов именно по отношению к этим криптоалгоритмам используют термин криптография, что вполне оправдано. Так, например, любой криптоалгоритм с ключом можно превратить в тайнопись, просто "зашив" в исходном коде программы некоторый фиксированный ключ. Обратное же преобразование практически невозможно.
В зависимости от характера воздействий, производимых над данными, алгоритмы подразделяются на:
Заметьте: любые криптографические преобразования не увеличивают объем информации, а лишь изменяют ее представление. Поэтому, если программа шифрования значительно (более, чем на длину заголовка) увеличивает объем выходного файла, то в ее основе лежит неоптимальный, а возможно и вообще некорректный криптоалгоритм. Уменьшение объема закодированного файла возможно только при наличии встроенного алгоритма архивации в криптосистеме и при условии сжимаемости информации (так, например, архивы, музыкальные файлы формата MP3, видеоизображения формата JPEG сжиматься более чем на 2-4% не будут).
В зависимости от размера блока информации криптоалгоритмы делятся на:
2.2.1. Скремблеры
Скремблерами называются программные или
аппаратные реализации
алгоритма, позволяющего шифровать побитно
непрерывные потоки
информации. Сам скремблер представляет из себя набор бит, изменяющихся
на каждом шаге по определенному алгоритму. После выполнения каждого
очередного шага на его выходе появляется шифрующий бит – либо 0, либо 1,
который накладывается на текущий бит информационного потока операцией XOR.
2.2.2. Блочные шифры
Блочные шифры шифруют целые блоки информации (от 4 до 32 байт) как единое
целое – это значительно увеличивает стойкость преобразований к атаке
полным перебором и позволяет использовать различные математические и
алгоритмические преобразования.
В последнее время сфера применения скремблирующих алгоритмов значительно сократилась. Это объясняется в первую очередь снижением объемов побитной последовательной передачи информации, для защиты которой были разработаны данные алгоритмы. Практически повсеместно в современных системах применяются сети с коммутацией пакетов, для поддержания конфиденциальности которой используются блочные шифры. А их криптостойкость превосходит, и порой довольно значительно, криптостойкость скремблеров.
Суть скремблирования заключается в побитном изменении проходящего через систему потока данных. Практически единственной операцией, используемой в скремблерах является XOR – "побитное исключающее ИЛИ". Параллельно прохождению информационного потока в скремблере по определенному правилу генерируется поток бит – кодирующий поток. Как прямое, так и обратное шифрование осуществляется наложением по XOR кодирующей последовательности на исходную.
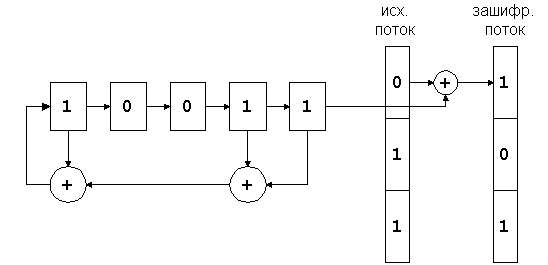
Генерация кодирующей последовательности бит производится циклически из небольшого начального объема информации – ключа по следующему алгоритму. Из текущего набора бит выбираются значения определенных разрядов и складываются по XOR между собой. Все разряды сдвигаются на 1 бит, а только что полученное значение ("0" или "1") помещается в освободившийся самый младший разряд. Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным ее битом (см. рис.1).

Рис.1.
Из теории передачи данных криптография заимствовала для записи подобных схем двоичную систему записи. По ней изображенный на рисунке скремблер записывается комбинацией "100112" – единицы соответствуют разрядам, с которых снимаются биты для формирования обратной связи.
Рассмотрим пример кодирования информационной последовательности 0101112 скремблером 1012 с начальным ключом 1102.
скремблер код.бит инф.бит рез-т
1 1 0 _
\ \ \_
1 1 1 _ \_
\ \ \_ 0 XOR 0 = 0
0 1 1 _ \_
\ \ \_ 1 XOR 1 = 0
1 0 1 \_
\ \ 1 XOR 0 = 1
и т.д.
Как видим, устройство скремблера предельно просто. Его реализация возможна как на электронной, так и на электрической базе, что и обеспечило его широкое применение в полевых условиях. Более того, тот факт, что каждый бит выходной последовательности зависит только от одного входного бита, еще более упрочило положение скремблеров в защите потоковой передачи данных. Это связано с неизбежно возникающими в канале передаче помехами, которые могут исказить в этом случае только те биты, на которые они приходятся, а не связанную с ними группу байт, как это имеет место в блочных шифрах.
Декодирование заскремблированных последовательностей происходит по той же самой схеме, что и кодирование. Именно для этого в алгоритмах применяется результирующее кодирование по "исключающему ИЛИ" – схема, однозначно восстановимая при раскодировании без каких-либо дополнительных вычислительных затрат. Произведем декодирование полученного фрагмента.
Как Вы можете догадаться, главная проблема шифров на основе скремблеров - синхронизация передающего (кодирующего) и принимающего (декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация необратимо теряется. Поэтому, в системах шифрования на основе скремблеров очень большое внимание уделяется методам синхронизации. На практике для этих целей обычно применяется комбинация двух методов: а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении такого бита активно начать поиск синхронизации с отправителем, и б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить декодирование принимаемых битов информации "по памяти" без синхронизации.
Число бит, охваченных обратной связью, то есть разрядность устройства памяти для порождающих кодирующую последовательность бит называется разрядностью скремблера. Изображенный выше скремблер имеет разрядность 5. В отношении параметров криптостойкости данная величина полностью идентична длине ключа блочных шифров, который будет проанализирован далее. На данном же этапе важно отметить, что чем больше разрядность скремблера, тем выше криптостойкость системы, основанной на его использовании.
При достаточно долгой работе скремблера неизбежно возникает его зацикливание. По выполнении определенного числа тактов в ячейках скремблера создастся комбинация бит, которая в нем уже однажды оказывалась, и с этого момента кодирующая последовательность начнет циклически повторяться с фиксированным периодом. Данная проблема неустранима по своей природе, так как в N разрядах скремблера не может пребывать более 2N комбинаций бит, и, следовательно, максимум, через, 2N-1 циклов повтор комбинации обязательно произойдет. Комбинация "все нули" сразу же исключается из цепочки графа состояний скремблера – она приводит скремблер к такому же положению "все нули". Это указывает еще и на то, что ключ "все нули" неприменим для скремблера. Каждый генерируемый при сдвиге бит зависит только от нескольких бит хранимой в данный момент скремблером комбинации. Поэтому после повторения некоторой ситуации, однажды уже встречавшейся в скремблере, все следующие за ней будут в точности повторять цепочку, уже прошедшую ранее в скремблере.
Возможны различные типы графов состояния скремблера. На рисунке 2 приведены примерные варианты для 3-разрядного скремблера. В случае "А" кроме всегда присутствующего цикла "000">>"000" мы видим еще два цикла – с 3-мя состояниями и 4-мя. В случае "Б" мы видим цепочку, которая сходится к циклу из 3-х состояний и уже никогда оттуда не выходит. И наконец, в случае "В" все возможные состояния кроме нулевого, объединены в один замкнутый цикл. Очевидно, что именно в этом случае, когда все 2N-1 состояний системы образуют цикл, период повторения выходных комбинаций максимален, а корреляция между длиной цикла и начальным состоянием скремблера (ключом), которая привела бы к появлению более слабых ключей, отсутствует.
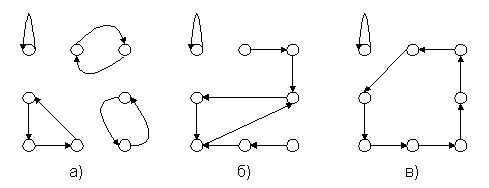
Рис.2.
И вот здесь математика преподнесла прикладной науке, каковой является криптография, очередной подарок. Следствием одной из теорем доказывается (в терминах применительно к скремблированию), что для скремблера любой разрядности N всегда существует такой выбор охватываемых обратной связью разрядов, что генерируемая ими последовательность бит будет иметь период, равный 2N-1 битам. Так, например, в 8-битном скремблере, при охвате 0-го, 1-го, 6-го и 7-го разрядов действительно за время генерации 255 бит последовательно проходят все числа от 1 до 255, не повторяясь ни разу.
Схемы с выбранными по данному закону обратными связями называются генераторами последовательностей наибольшей длины (ПНД), и именно они используются в скремблирующей аппаратуре. Из множества генераторов ПНД заданной разрядности во времена, когда они реализовывались на электрической или минимальной электронной базе выбирались те, у которых число разрядов, участвующих в создании очередного бита, было минимальным. Обычно генератора ПНД удавалось достичь за 3 или 4 связи. Сама же разрядность скремблеров превышала 30 бит, что давало возможность передавать до 240 бит = 100 Мбайт информации без опасения начала повторения кодирующей последовательности.
ПНД неразрывно связаны с математической теорией неприводимых полиномов. Оказывается, достаточно чтобы полином степени N не был представим по модулю 2 в виде произведения никаких других полиномов, для того, чтобы скремблер, построенный на его основе, создавал ПНД. Например, единственным неприводимым полиномом степени 3 является x3+x+1, в двоичном виде он записывается как 10112 (единицы соответствуют присутствующим разрядам). Скремблеры на основе неприводимых полиномов образуются отбрасыванием самого старшего разряда (он всегда присутствует, а следовательно, несет информацию только о степени полинома), так на основе указанного полинома, мы можем создать скремблер 0112 с периодом зацикливания 7(=23-1). Естественно, что на практике применяются полиномы значительно более высоких порядков. А таблицы неприводимых полиномов любых порядков можно всегда найти в специализированных математических справочниках.
Существенным недостатком скремблирующих алгоритмов является их нестойкость к фальсификации. Подробнее данная проблема рассмотрена на следующей лекции, применительно к созданию целых криптосистем.
2.2.2.1. Общие сведения о блочных шифрах
На сегодняшний день разработано достаточно много стойких блочных шифров.
Практически все алгоритмы используют для преобразований определенный
набор биективных (обратимых) математических преобразований
2.2.2.2. Сеть Фейштеля
Сетью Фейштеля называется метод обратимых
преобразований текста, при котором
значение, вычисленное от одной из частей текста, накладывается на другие
части. Часто структура сети выполняется таким образом, что для шифрования
и дешифрования используется один и тот же алгоритм – различие состоит
только в порядке использования материала ключа.
2.2.2.3. Блочный шифр TEA
Блочный алгоритм TEA приведен как пример одного
из самых простых в реализации стойких криптоалгоритмов.
2.2.2.4. AES : cтандарт блочных шифров США
c 2000 года
В 1998 году был объявлен открытый конкурс на криптостандарт США на несколько
первых десятилетий XXI века. Победителем конкурса был признан бельгийский
блочный шифр Rijndael. Скорее всего он станет
стандартом де-факто блочного шифрования во всем мире.