2.3.3. Методы рандомизации сообщений

2.3.3.1. Обзор методик рандомизации сообщений
Две основные методики внесения случайности в процесс шифрования представляют из себя: а) внесение случайных бит в сам шифруемый файл с игнорированием их на дешифрующей стороне, б) шифрование исходного файла случайным ключом.

2.3.3.2. Генераторы случайных и псевдослучайных последовательностей
Генераторы случайных последовательностей играют большую роль в современной криптографии. В том случае, когда генерируемая последовательность основана только на состоянии ЭВМ, она называется псевдослучайной. Действительно случайными являются только некоторые физические процессы и человеческий фактор.

2.3.3.1. Обзор методик рандомизации сообщений

Следующим усовершенствованием, направленным на повышение стойкости всей системы в целом является создание ключей сеанса. Эта операция необходима в тех случаях, когда производится частое шифрование сходных блоков данных одним и тем же ключом. Например, это имеет место при передаче информации или команд в автоматизированных системах управления, в банковских операциях и многих других случаях передачи информации, имеющей определенный заранее известный формат.

В этом случае необходимо введение какой-либо случайной величины в процесс шифрования. Это можно сделать несколькими способами:

записью в начало файла данных псевдослучайной последовательности байт заранее оговоренной длины с отбрасыванием ее при дешифровании – этот метод будет работать только при применении алгоритмов создания цепочек с памятью (CBC,CFB,OFB),
применением модифицированных алгоритмов создания цепочек, которые при шифровании каждого блока смешивают с ним либо а) фиксированную случайную величину, прикрепленную к началу зашифрованного файла, либо б) значения (значение), вычисляемые с помощью того же шифра и ключа от заранее оговоренной величины,
созданием специально для каждого файла совершенно случайного ключа, так называемого ключа сеанса, которым и шифруется весь файл (сам же ключ сеанса шифруется первоначальным ключом, называемым в этом случае мастер-ключом и помещается в начале зашифрованного файла).

Все схемы принципиально не имеют очевидных недостатков, но из-за большей проработанности последнего метода обычно применяется именно он.

2.3.3.2. Генераторы случайных и псевдослучайных последовательностей

Самая большая проблема всех методов рандомизации сообщений – это порождение действительно случайной последовательности бит. Дело в том, что генераторы случайных последовательностей, используемые для общих целей, например, в языках программирования, являются на самом деле псевдослучайными генераторами. Дело в том, что в принципе существует конечное, а не бесконечное множество состояний ЭВМ, и, как бы сложно не формировалось в алгоритме число, оно все равно имеет относительно немного бит информационной насыщенности.

Давайте рассмотрим проблему создания случайных и псевдослучайных чисел более детально. Наиболее часто в прикладных задачах результат формируют из счетчика тиков – системных часов. В этом случае данные о текущем часе несут примерно 16 бит информации, значение счетчика тиков – еще 16 бит. Это дает нам 32 бита информации – как вы помните, на сегодняшний день границей стойкой криптографии является значение в 40 бит, при реальных длинах ключей в 128 бит. Естественно, подобного метода крайне недостаточно. Идем дальше, к 32 битам можно добавить еще 16 бит из сверхбыстрого таймера, работающего на частоте 1,2 МГц в компьютерах архитектуры IBM PC AT и этого еще недостаточно. Кроме того, даже если мы сможем набрать длину ключа в 128 бит (что очень сомнительно), она будет нести псевдослучайный характер, поскольку основана на состоянии только лишь данной ЭВМ на момент начала шифрования. Источниками по-настоящему случайных величин могут быть только внешние объекты, например, человек.

Два наиболее часто применяемых метода создания случайных последовательностей с помощью человека основаны на вводе с клавиатуры. В обоих случаях пользователя просят, не задумываясь, понабирать на клавиатуре бессмысленные сочетания букв.

По первому методу над самими введенными значениями производятся действия, повышающие случайность выходного потока. Так, например, обязательно удаляются верхние 3 бита введенного ASCII символа, часто удаляются еще один верхний и еще один нижний биты. Затем, объем полученной последовательности уменьшается еще в три раза наложением первого и второго бита на третий операцией XOR. Это, в принципе, генерирует достаточно случайную последовательность бит.

По второму методу на введенные символы алгоритм не обращает никакого внимания, зато конспектирует интервалы времени, через которые произошли нажатия. Запись моментов производится по отсчетам быстрого системного таймера (частота 1,2 МГц) или внутреннему счетчику процессора, появившемуся в процессорах, начиная с Intel Pentium (частота соответствует частоте процессора). Так как верхние и младшие биты имеют определенную корреляцию между символами (первые из-за физических характеристик человека, вторые из-за особенностей операционной системы), то они отбрасываются (обычно удаляются 0-8 старших бита и 4-10 младших).

Как более редко встречающиеся варианты можно встретить 1) комбинацию обоих клавиатурных методов и 2) метод, основанный на манипуляторе "мышь" - он выделяет случайную информацию из смещений пользователем указателя мыши.

В мощных криптосистемах военного применения используются действительно случайные генераторы чисел, основанные на физических процессах. Они представляют собой платы, либо внешние устройства, подключаемые к ЭВМ через порт ввода-вывода. Два основных источника белого Гауссовского шума – высокоточное измерение тепловых флуктуаций и запись радиоэфира на частоте, свободной от радиовещания.

2.3.4. Архивация

2.3.4.1. Общие принципы архивации. Классификация методов
Существуют две большие группы алгоритмов архивации: сжатие без потерь биективно перекодирует информацию по другим законам, то есть возможно абсолютно идентичное ее восстановление; сжатие с потерями необратимо удаляет из информации некоторые сведения, оказывающие наименьшее влияние на смысл сообщения.

2.3.4.2. Алгоритм Хаффмана
Алгоритм сжатия ориентирован на неосмысленные последовательности символов какого-либо алфавита. Необходимым условием для сжатия является различная вероятность появления этих символов (и чем различие в вероятности ощутимее, тем больше степень сжатия).

2.3.4.3. Алгоритм Лемпеля-Зива
А этот алгоритм сжатия основан наоборот на корреляциях между расположенными рядом символами алфавита (словами, управляющими последовательностями, заголовками файлов фиксированной структуры).

2.3.4.1. Общие принципы архивации. Классификация методов

Следующей большой темой является архивация данных. Как Вам известно, подавляющее большинство современных форматов записи данных содержат их в виде, удобном для быстрого манипулирования, для удобного прочтения пользователями. При этом данные занимают объем больший, чем это действительно требуется для их хранения. Алгоритмы, которые устраняют избыточность записи данных, называются алгоритмами сжатия данных, или алгоритмами архивации. В настоящее время существует огромное множество программ для сжатия данных, основанных на нескольких основных способах.

Зачем же нужна архивация в криптографии? Дело в том, что в современном криптоанализе, то есть науке о противостоянии криптографии, с очевидностью доказано, что вероятность взлома криптосхемы при наличии корреляции между блоками входной информации значительно выше, чем при отсутствии таковой. А алгоритмы сжатия данных по определению и имеют своей основной задачей устранение избыточности, то есть корреляций между данными во входном тексте.

Все алгоритмы сжатия данных качественно делятся на 1) алгоритмы сжатия без потерь, при использовании которых данные на приемной восстанавливаются без малейших изменений, и 2) алгоритмы сжатия с потерями, которые удаляют из потока данных информацию, незначительно влияющую на суть данных, либо вообще невоспринимаемую человеком (такие алгоритмы сейчас разработаны только для аудио- и видео- изображений). В криптосистемах, естественно, используется только первая группа алгоритмов.

Существует два основных метода архивации без потерь:

алгоритм Хаффмана (англ. Huffman), ориентированный на сжатие последовательностей байт, не связанных между собой,
алгоритм Лемпеля-Зива (англ. Lempel, Ziv), ориентированный на сжатие любых видов текстов, то есть использующий факт неоднократного повторения "слов" – последовательностей байт.

Практически все популярные программы архивации без потерь (ARJ, RAR, ZIP и т.п.) используют объединение этих двух методов – алгоритм LZH.

2.3.4.2. Алгоритм Хаффмана

Алгоритм основан на том факте, что некоторые символы из стандартного 256-символьного набора в произвольном тексте могут встречаться чаще среднего периода повтора, а другие, соответственно, – реже. Следовательно, если для записи распространенных символов использовать короткие последовательности бит, длиной меньше 8, а для записи редких символов – длинные, то суммарный объем файла уменьшится.

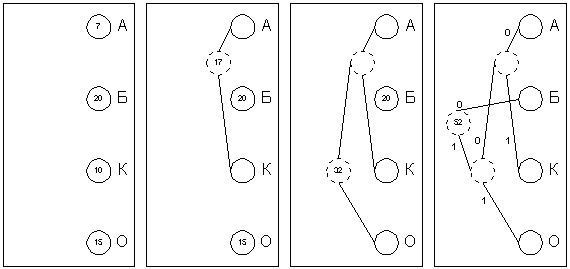
Хаффман предложил очень простой алгоритм определения того, какой символ необходимо кодировать каким кодом для получения файла с длиной, очень близкой к его энтропии (то есть информационной насыщенности). Пусть у нас имеется список всех символов, встречающихся в исходном тексте, причем известно количество появлений каждого символа в нем. Выпишем их вертикально в ряд в виде ячеек будущего графа по правому краю листа (рис. 1а). Выберем два символа с наименьшим количеством повторений в тексте (если три или большее число символов имеют одинаковые значения, выбираем любые два из них). Проведем от них линии влево к новой вершине графа и запишем в нее значение, равное сумме частот повторения каждого из объединяемых символов (рис.2б). Отныне не будем принимать во внимание при поиске наименьших частот повторения два объединенных узла (для этого сотрем числа в этих двух вершинах), но будем рассматривать новую вершину как полноценную ячейку с частотой появления, равной сумме частот появления двух соединившихся вершин. Будем повторять операцию объединения вершин до тех пор, пока не придем к одной вершине с числом (рис.2в и 2г). Для проверки: очевидно, что в ней будет записана длина кодируемого файла. Теперь расставим на двух ребрах графа, исходящих из каждой вершины, биты 0 и 1 произвольно – например, на каждом верхнем ребре 0, а на каждом нижнем – 1. Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до нее, выписывая нули и единицы по маршруту следования. Для рисунка 4.5 символ "А" получает код "000", символ "Б" – код "01", символ "К" – код "001", а символ "О" – код "1".

Рис.1.

В теории кодирования информации показывается, что код Хаффмана является префиксным, то есть код никакого символа не является началом кода какого-либо другого символа. Проверьте это на нашем примере. А из этого следует, что код Хаффмана однозначно восстановим получателем, даже если не сообщается длина кода каждого переданного символа. Получателю пересылают только дерево Хаффмана в компактном виде, а затем входная последовательность кодов символов декодируется им самостоятельно без какой-либо дополнительной информации. Например, при приеме "0100010100001" им сначала отделяется первый символ "Б" : "01-00010100001", затем снова начиная с вершины дерева – "А" "01-000-10100001", затем аналогично декодируется вся запись "01-000-1-01-000-01" "БАОБАБ".

2.3.4.3. Алгоритм Лемпеля-Зива

Классический алгоритм Лемпеля-Зива – LZ77, названный так по году своего опубликования, предельно прост. Он формулируется следующим образом : "если в прошедшем ранее выходном потоке уже встречалась подобная последовательность байт, причем запись о ее длине и смещении от текущей позиции короче чем сама эта последовательность, то в выходной файл записывается ссылка (смещение, длина), а не сама последовательность". Так фраза "КОЛОКОЛ_ОКОЛО_КОЛОКОЛЬНИ" закодируется как "КОЛО(-4,3)_(-5,4)О_(-14,7)ЬНИ".

Распространенный метод сжатия RLE (англ. Run Length Encoding), который заключается в записи вместо последовательности одинаковых символов одного символа и их количества, является подклассом данного алгоритма. Рассмотрим, например, последовательность "ААААААА". С помощью алгоритма RLE она будет закодирована как "(А,7)", в то же время ее можно достаточно хорошо сжать и с помощью алгоритма LZ77 : "А(-1,6)". Действительно, степень сжатия именно такой последовательности им хуже (примерно на 30-40%), но сам по себе алгоритм LZ77 более универсален, и может намного лучше обрабатывать последовательности вообще несжимаемые методом RLE.